Cây khung (Spanning Tree) là gì?
Một cây khung là một tập con của Grahp G mà có tất cả các đỉnh được bao bởi số cạnh tối thiểu nhất. Vì thế, một cây khung sẽ không hình thành một vòng tuần hoàn và nó cũng không thể bị ngắt giữa chừng.
Từ định nghĩa trên ta có thể kết luận rằng mỗi Graph G tuần hoàn sẽ có ít nhất một cây khung. Một Graph G bị ngắt giữa chừng sẽ không có bất kỳ cây khung nào.
Dưới đây là hình ví dụ minh họa cho một Grahp G và các cây khung của nó:
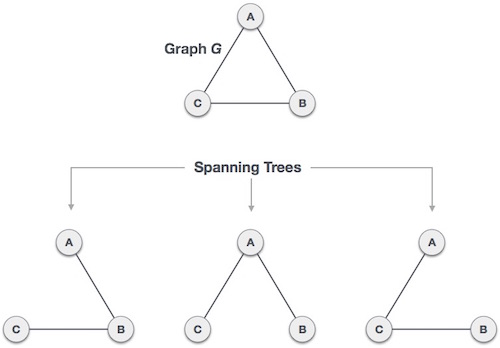
Ở trên chúng ta có 3 cây khung của một đồ thị tuần hoàn. Một đồ thị tuần hoàn có thể có tối đa nn-2 cây khung, trong đó n là số nút. Trong ví dụ trên, n là 3 do đó 33−2 = 3 cây khung.
Thuộc tính chung của cây khung (Spanning Tree)
Bây giờ chúng ta hiểu rằng một Graph có thể có nhiều hơn một cây khung. Phần dưới đây là một số thuộc tính của cây khung của Graph G tuần hoàn đã cho:
Một Grahp G tuần hoàn có thể có nhiều hơn một cây khung.
Tất cả các cây khung của một Graph G đều có cùng số cạnh và số đỉnh.
Cây khung không có bất kỳ vòng tuần hoàn nào.
Việc xóa một cạnh từ cây khung sẽ làm cho Grahp là không tuần hoàn.
Thêm một cạnh vào cây khung sẽ tạo nên một vòng tuần hoàn.
Thuộc tính toán học của cây khung (Spanning Tree)
Cây khung có n-1 cạnh, trong đó n là số nút (đỉnh).
Từ một Graph tuần hoàn, bằng việc xóa đi tối đa e-n+1 cạnh, chúng ta có thể xây dựng một cây khung.
Một Grahp tuần hoàn có thể có tối đa nn-2 cây khung.
Ứng dụng của cây khung (Spanning Tree)
Về cơ bản cây khung được sử dụng để tìm các đường ngắn nhất để kết nối tất cả các nút trong một Graph. Các ứng dụng phổ biến của cây khung là:
- Lập kế hoạch mạng dân sự
- Giao thức định tuyến mạng máy tính
- Cluster Analysis
Chúng ta tìm hiểu ví dụ đơn giản sau để hiểu các ứng dụng này. Bạn thử tưởng tượng một mạng internet trong thành phố là một hình Graph lớn và bây giờ kế hoạch đặt ra là triển khai các đường dây mạng sao cho với độ dài dây là ngắn nhất mà vẫn có thể kết nối được tất cả các nút trong thành phố. Đó là một ví dụ giải thích cho ứng dụng của cây khung.
Cây khung nhỏ nhất (Minimum Spanning Tree – MST)
Trong một đồ thị có trọng số (Weighted Graph), một cây khung nhỏ nhất là cây khung mà có trọng số (weight) nhỏ nhất trong tất cả các cây khung của Grahp này. Trong đời sống thực, weight (trọng số) ở đây có thể là khoảng cách (distance), độ nghẽn (congestion), độ tải (traffic load) hoặc bất kỳ giá trị nào có thể được biểu diễn thành các cạnh.
Giải thuật cho cây khung nhỏ nhất
Bởi vì giới hạn về độ dài trang, mình sẽ không trình bày hai giải thuật sau trong chương này. Mời các bạn click chuột vào hai đường dẫn dưới đây để tiếp tục tìm hiểu hai giải thuật cây khung quan trọng nhất:
- Giải thuật cây khung nhỏ nhất của Kruskal
- Giải thuật cây khung nhỏ nhất của Prim
Theo Tutorialspoint
Bài trước: Cây AVL trong cấu trúc dữ liệu và giải thuật
Bài tiếp: Cấu trúc dữ liệu Heap












